前面我們提過了 decision tree 這個東西，今天來提一下 tree structure
來為接下來的 heap sort 做準備

What is tree

1. Used to represent hierarchical data
   Trees are ideal for representing hierarchical data, such as file systems, organizational structures, and more.
2. Starts at a single point, called the root
   The tree begins with a root node, which serves as the starting point of the structure. Each tree must have exactly one root.
3. Each node can have zero, one or multiple child nodes, and all nodes except the root must have one parent.
   A tree's nodes are connected through parent-child relationships, where each node have multiple children but only one parent(except for the root).
4. Must not have loops
   Trees are acyclic structures, meaning they cannot have cycles or loops-there is only one path between any two nodes.
5. Edges
   The lines that connect nodes are called edge, representing relationships between nodes.
6. Leaves
   The nodes at the bottommost level of a tree, which do not have any children, are referred to as leaves.

1. tree 是用來表示階層關係的資料結構
2. 所有tree都源自於單一個節點稱作 root，此節點沒有 parent node
3. 一個節點本身可以有一個、零個或多個子節點，但只能有一個 parent node
4. tree 內不可以有 loops
5. 連接節點跟節點的線稱為 edge 用來表現 node 之間的關係
6. 最底端的節點沒有任何的子節點，稱之為leaf(複數型 leaves)

Example of tree and non-trees

example of a tree

non-tree

Type of trees

Binary tree

A tree data structure that each node has most two children node.
These children are usually refered to as the left child and right child.

樹狀結構的 parent node 至多有兩個 child node 則稱作二元樹(Binary tree)，child node 分別稱為左節點(left child)與右節點(right child)

• Complete binary tree
  A complete binary tree is a binary tree in which all levels are fully filled except the last, and all nodes are as far left as possible.
  除了最底層的節點未完全填滿，且最底層節點盡可能向左靠攏的二元樹又可稱為 complete binary tree
  

• Full binary tree
  A full binary tree is a binary tree where every node has either 0 or 2 children(no nodes have only one child)

除了最底層節點沒有子節點外，其他節點均有零或兩個子節點的二元樹又可稱為 full binary tree

Ternary tree

A tree data structure that each node has most three children node.
These children are usually refered to as the left child , middle child and right child.

樹狀結構的 parent node 至多有三個 child node 則稱作三元樹(Binary tree)，child node 分別稱為左節點(left child),中節點(middle child)與右節點(right child)

A ternary tree of size 10 and height 2
以下圖為高度2層，大小為10的三元樹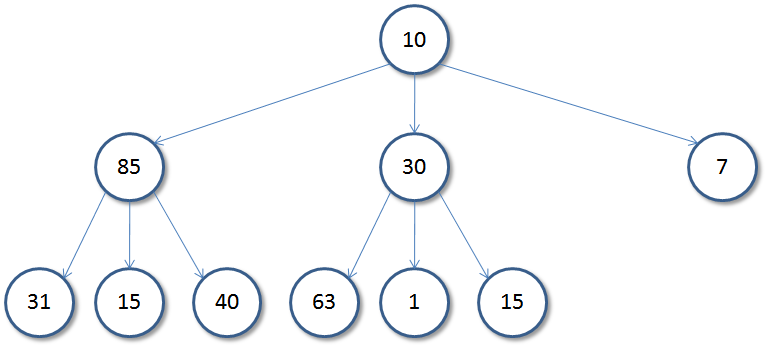

圖片來源

用 js 建立 binary search tree

Binary Search tree，顧名思義是 binary tree 的一種，其特色為
越小的值越靠左邊堆積，越大的值會越靠右邊堆積

• 左子樹（left Subtree）中任意節點的值都小於其父節點（parent node）
• 右子樹（right Subtree）中任意節點的值都大於其父節點（parent node）
• 左右子樹本身及其子樹都是 binary search tree

完整程式碼在這裡
首先，先建立 Node(單一節點)，每個binary tree內的節點都會有兩個children node(left & right)

class Node{
    constructor(value){
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

建立 class of binaryTree ，其default value of root 為 null

class binaryTree {
    constructor(){
        this.root = null;
    }
}

對此tree 新增節點的方法 insert
tree 並不像 array 可以直接用 length 遍歷，需要從一個節點移動到下個節點

如果此 tree 沒有 root => 該 Node 則為 root Node
如果此 tree 有 root => 移動到 root Node 並比較 insert value 與 value of root的大小，藉此決定往左邊 insert 或往右邊 insert

class binaryTree {
    constructor(){
        this.root = null;
    }
    
    insert(value) {
    let newNode = new Node(value);
    if (!this.root) {
      this.root = newNode;
      return this;
    }

    let currentNode = this.root;
    while (true) {
      if (value < currentNode.value) {
        if (!currentNode.left) {
          currentNode.left = newNode;
          return this;
        }
        currentNode = currentNode.left;
      } else {
        if (!currentNode.right) {
          currentNode.right = newNode;
          return this;
        }
        currentNode = currentNode.right;
      }
    }
    return this;
  }
    
}

相關資源

Tree
https://en.wikipedia.org/wiki/Tree_(abstract_data_type)
Trees In Data Structure
https://www.youtube.com/watch?v=9oTV7fDEaCY
ternary tree
https://en.wikipedia.org/wiki/Ternary_tree
full binary tree vs complete binary tree
https://www.javatpoint.com/full-binary-tree-vs-complete-binary-tree